The theology of the Sphere is prescribed by its topology
MatematicaAnyone who believes in a substantial unity of the culture cannot avoid to refuse as definitely artificial the opposition of (the so called) sciences to (the so called) humanities. The sciences are human and we contend that humanities can be studied through the methods of the most rigorous sciences. Believing that they are split by a wall, unavoidably leads to big disasters: people may turn unaware that the culture is one crucial key to improve the general wellness.
The purpose of this short note is not to provide theoretical arguments to investigate a question that is probably as old as the appearance of the rational thought, but to support our firm trusting in the unity of the culture, through a couple of relevant examples. They will be borrowed from topology, one of the purest branches among pure mathematics, which is in turn the most exact among exact sciences. This will show, the author thinks, an unsuspected link between pure maths and theology. Yes theology! Topology1 is concerned with the art of shaping the space, by studying the properties that remain untouched under continuous deformations. It is also known as the rubber sheet geometry.
Continuous deformation of a sphere to an “ovoid”
Theology, instead, is concerned with God, an almighty being Who has designed the universe according to almighty wishes but could have drawn it in a different way. The question is: with how much freedom?
This is the right moment to mention the following couple of (physical?) facts. The First. On the surface of the Earth, at each given instant time, there is a pair of antipodal points with the same temperature and the same atmospherical pressure, i.e. at least two points, at the antipodes, with exactly the same weather. The second. On the Earth surface, crossed by winds, there are always quiet spots, namely points where the winds do not blow. Are these Nature’s law? Is it possible to imagine a Universe, or many universes (pluriverses?) where such laws do not hold for some planet?
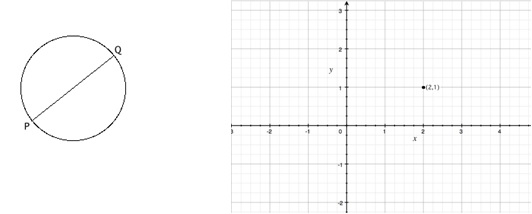
Let us begin to cope with the first “meteorological” situation. In the obscure times of the Second World War, two poolish mathematicians, Karol Borsuk (1905-1982) and Stanislaw Ulam (1909-1984, who also participated to the famous Manhattan project, devoted to the realization of the first atomic bomb), stated and proved an astonishing theorem. Recall: a theorem is a proposition whose truth must be validated by a rigorous proof. In a simplified form, Borsuk and Ulam’s result2 says that every continuous function from the sphere to the plane takes the same value at least to one pair of antipodal points. Let us explain to non-mathematicians what this does mean. Recall: two points of a spherical surface are said to be antipodal if they are diametrically opposed (one usually says that Italy and Australia are antipodal). Since the points of a plane can be labeled by pairs of real numbers, as depicted in the figure below, to give a function from the sphere to the plane is the same as labeling all the points of its surface by a pair of real numbers (that supplies the correspondence to a point of the plane).
For better explanation, it can be helpful going directly to the example. Consider the “function” associating to each point of the Earth, thought of as a physical model of a sphere, its pressure and its temperature. This is a function with values in a plane, because to each point of the sphere one is attaching a point in the “pressure – temperature” diagram. What does it mean that such a function is continuous? Roughly speaking, it means that if a point of the sphere has a given pressure and temperature (P,T), there are neighboring points whose labeling pairs (pressure, temperature) differ from the given data as little as one desires. Putting otherwise, although not completely correct, it means that if we move in a close neighbourhood of the point, there is a little variation of the pressure and of the temperature.
Two antipodal points on a Sphere’s surface The point represented by the bullet has been labeled with (2,1)
The issue is now: how to guarantee that pressure and temperature vary continuously with the position? This is not proven. This is Faith. Better, it is metaphysics. We trust that (physicists do) basing upon experimental (but possibly failing) evidence. And assuming continuity, Borsuk and Ulam ensure us that there MUST be two antipodal points on the sphere with the same pressure and temperature, just because the function {point of the sphere}—>(its temperature, its pressure) is continuous by hypothesis. In other words: there are two antipodal points on the Earth with the same weather!
The second phenomenon we want to mention is that of the eye(s) of the storm(s), the point, or the points, on the Earth surface where there is no wind blowing. The existence of such spots is a necessary consequence of the topology of the sphere as well. It is related with the following classical purely topological theorem: there is no tangent vector field on a sphere that does not vanish to at least one point (indeed, it vanishes to at least two points). What is a tangent vector field? The wind is an example. But you can also think to the hairs of the head. You can think of each hair as if it were a model of a vector (in college physics books they are usually represented by arrows, having a magnitude and a verse, used to describe forces or physical fields). So, you can think of the set of all hairs on your head as a model of a vector field. If you are hair bumped, then the vector field is not tangent. But if you comb your hairs you may turn them into a tangent vector field
A non tangent vector field A tangent vector field: can you distinguish an eye of the storm?
The aforementioned theorem then claims that the sphere is not a combable surface: imagine to be given a radial field of “hairs”, one at each point of a sphere. The theorem demands that to completely comb it, you must remove at least two hairs (points where the “hairs” tangent vector field vanishes). As a consequence, any continuous wind vector field on a sphere’s surface, MUST vanish to at least two (may be more, but at least two) points where the wind does not blow. These are the eyes of storms.
Combing a sphere Eye of the storm
In conclusion, it seems that mathematics is able to impose laws to Nature, like e.g the same weather at two antipodal points or, as seen, the eyes of storms irrevocably destined to be attached to a winds’ field. Have they to be considered as Nature’s laws? Or they rather are necessary ones, unavoidable ones? The reader may object that the Earth is not a perfect sphere. But that does not matter, you know. This is topology, whose properties hold for all surfaces that can be continuously deformed one into another. If X can be continuously changed into a sphere (imaging it made of a sort of magic rubber that can be deformed and shape at anyone own wish) then a) a plane valued continuous function on X must take the same values to at least one pair of distinct points and b) any tangent vector field must vanish to at least two points (you cannot comb it completely).
To come to the theological impact we ask ourselves: are the aforementioned results prescribing any kind of limitation to the power of God? Think a little bit about. The discussed theorems are saying us that God (or the Nature) can create universes where temperature and pressure, or wind blowing, may not vary continuously on a sphere’s surface. That is possible, of course. However, if continuity is preserved and/or demanded, He cannot prevent that at least one pair of antipodal points take the same temperature and pressure and He cannot avoid a wind having his own eye of storm. Mathematics is thus prescribing, in these occurrences, laws concerning not the Pangloss’3 best possible World, but rather a rule that must be necessarily obeyed in all the possible worlds. As we have argued, the necessity of mathematics constrains the possibilities of Physics. This is quite striking.
Eventually, we believe that who does not stop a little bit to taste the magic flavor of theorems like that of Borsuk and Ulam, to reflect about the necessaries laws of an over-Nature that sometimes overcomes the empirical step of the scientific investigation, is going to loose the human, very human, too human side of the Science. He will loose all the fun which is the true joy of the scientific research. “There are more things in Heaven and Earth, Horatio, than are dreamt of in your philosophy”4. Nowadays, we could phrase Hamlet’s warning as “there are many more interesting questions than boring anwers”. Not just general, negligible questions, but queries that are relevant to our everyday life, to our beliefs, to our faiths, to our dreams.
Bibliographical Notes
1 For a general elementary and substantially self contained introduction to topology, see the book by Wallace, An Introduction to Algebraic Topology (Dover Books on Mathematics).
2 The theorem of Borsuk and Ulam is one of the most popular theorems in topology. Several readable accounts have been published. See e.g. the book by Massey, A basic course in Algebraic topology, Springer GTM 127.
3 Voltaire, Candide.
4 W. Shakespeare, Hamlet, Act 1, Scene 5.